评估方法

发表于 更新于 阅读次数：

混淆矩阵、准确率、精确率、召回率、F值、ROC曲线、AUC、PR曲线-Sklearn.metrics评估方法

混淆矩阵

  • TN ：真实为0，预测为0
  • FP ：真实为0，预测为1
  • FN ：真实为1，预测为0
  • TP ：真实为1，预测为1
混淆矩阵 预测
0 1
真实 0 TN FP
1 FN TP 
1
2
3
4
from sklearn.metrics import confusion_matrix
yp = [1,1,0,1,1,0,0,0,0,1]
yr = [1,1,1,1,1,0,0,1,0,0]
confusion_matrix=confusion_matrix(yr,yp)

output:

[[3 1]
[2 4]]

分类准确率 Accuracy

Accuracy是最常见的evaluation metric。但在binary classification中，如果遇见正反例不平衡的情况下，尤其是我们对少数类别感兴趣的情况下，Accuracy将不再具有参考价值。

比如，100个样本中有99个正例，那么我们全部预测为1，则准确率将达到99%。若将该model放在新样本环境中，却一个负例都无法分辨，使得该model毫无意义。

  • 所有样本中预测正确的比率

$$
Accuracy = \frac{TP+TN}{TN+FP+FN+TP}
$$

1
2
3
4
from sklearn.metrics import accuracy_score
yp = [1,1,0,1,1,0,0,0,0,1]
yr = [1,1,1,1,1,0,0,1,0,0]
accuracy_score=accuracy_score(yr,yp)

accuracy_score = 0.7

精确率 Precision

在所有预测为1的样本中，真实为1的概率。

你有一个model，期间预测了100个正样本，其中有90个为真的正样本，10个为假的正样本（预测错误）。精确度就是90%。
所以，精确度就是衡量一个model的可信度。

$$
Precision = \frac{TP}{TP+FP}
$$

1
2
from sklearn.metrics import precison_score
precison_score=precison_score(yr,yp)

precison_score = 0.8

召回率 Recall

在所有真实正样本中，正确预测出正样本的比率。
有一model，有100个真实正样本，model预测出80个正样本，20个负样本。因此召回率为80%

也就是说，召回率是表示model识别正样本的能力
$$
Recall = \frac{TP}{TP+FN}
$$

1
2
from sklearn.metrics import recall_score
recall_score=recall_score(yr,yp)

recall_score = 0.6666666666666666

其中Recall是相对真实答案而言的， Precision是相对model而言。

一般来说Precision与Recall是一种博弈的关系。

Recall高的，一般Precision就会低，因为model要考虑到更多的样本，就代表出错的可能性就越高。

反之，Precision高的，Recall一般会低，因为model只对它自己肯定的样本进行预测，这样一来model的泛华能力比较弱。
因此，就有了下面的F1 score，对这两个指数进行综合考察。

F1值

用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的准确率和召回率。F1分数可以看作是模型准确率和召回率的一种加权平均，它的最大值是1，最小值是0。

其中F1 score是一个综合考虑Precision和Recall的metric。
$$
F1 = 2\frac{PrecisonRecall}{Precision+Recall}
$$

1
2
from sklearn.metrics import f1_score
f1_score=f1_score(yr,yp)

f1_score = 0.7272727272727272

ROC曲线

计算ROC前 我们需要了解两个变量FPR（横轴）和TPR（纵轴）。

FPR (False Positive Rate)假阳性率：真实的反例中，被预测为正例的比率

TN+FP 为样本中所有负例的个数
$$
FPR = \frac{FP}{TN+FP}
$$
TPR (True Positive Rate)真阳性率: 真实的正例中，被预测为正例的比率

TP+FN 为样本中所有正例的个数
$$
TPR = \frac{TP}{TP+FN}
$$
理想分类器下 FPR=0，TPR=1。

其中，ROC曲线越接近左上角越好。

1
2
3
4
5
6
7
8
9
10
11
12
fpr, tpr, thresholds = metrics.roc_curve(yr,yp)
roc_auc = auc(fpr, tpr)  #auc为Roc曲线下的面积，计算auc
#开始画ROC曲线
plt.plot(fpr, tpr, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.1])
plt.ylim([-0.1,1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()
ROC

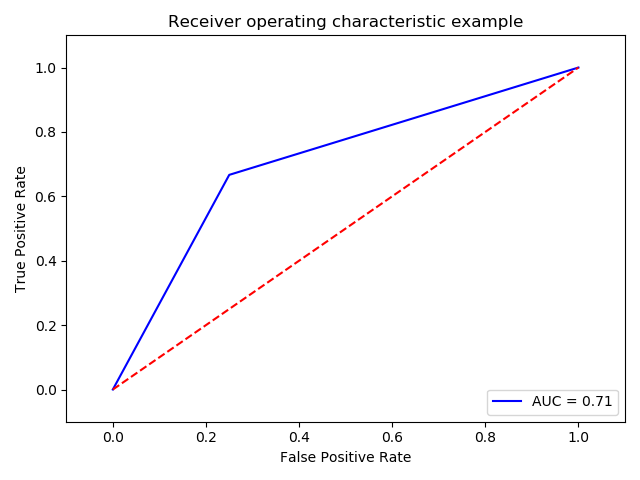
AUC

AUC指的是ROC曲线下方的面积。也是通过ROC曲线衡量模型好坏的一个重要指标，AUC的值越大越好。

在进行学习器的比较时，若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者；若两个学习器的ROC曲线发生交叉，则难以一般性的断言两者孰优孰劣。此时如果一定要进行比较，则比较合理的判断依据是比较ROC曲线下的面积，即AUC(Area Under Curve)。

PRC曲线

就是Precison和Recall分别为纵、横轴，根据不同的阈值画出的曲线，类似ROC。但与ROC不同的是，PRC曲线越接近右上角越好。同样，AUC越大越好。

1
2
3
4
5
6
7
8
9
10
11
p, r, thresholds = metrics.precision_recall_curve(yr,yp)
roc_auc = auc(r, p)  #auc为Roc曲线下的面积
#开始画ROC曲线
plt.plot(r, p, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
plt.xlim([-0.1,1.1])
plt.ylim([-0.1,1.1])
plt.xlabel('Recall') #横坐标是Recall
plt.ylabel('Precision')  #纵坐标是Precision
plt.title('PR example')
plt.show()
PR

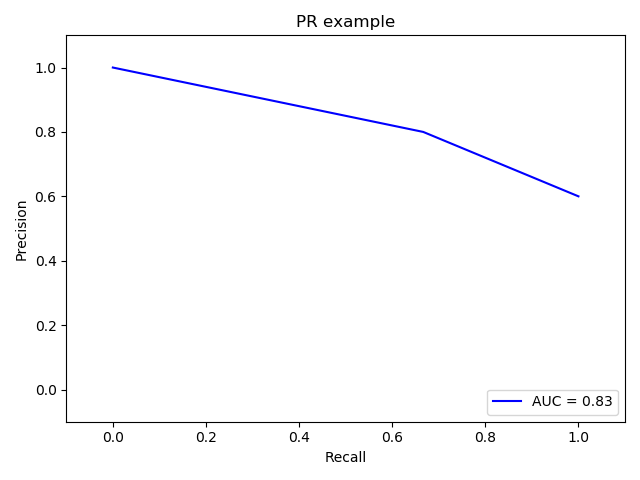
以上几个metric中ROC和PRC主要可以解决样本不平衡导致metric不可信的问题。
具体需要使用哪个metric具体模型具体分析。
但通过大量的实验表明：

在negative instances的数量远远大于positive instances的data set里， PRC更能有效衡量检测器的好坏。

参考：

https://www.zhihu.com/question/30643044/answer/48955833